第 7 章 线性模型和广义线性模型
线性模型是实际应用中最常用的统计模型。
7.1 模型假设
7.1.1 线性模型假设
经典线性模型的应用是有前提条件的。自变量 \(x = (x_1, ..., x_p)^T\) 被看做是给定的,而因变量 \(Y\) 来自均值为 \(μ\),方差为 \(σ^2\) 的正态分布 \(N(μ, σ^2)\),其中 \(μ\) 与 自变量 \(x\) 的关系是:
\[μ = \alpha + x^T\beta = \alpha + \beta_1x_1 + ... + \beta_px_p\]
这里回归系数 \(\alpha\) 是截距项,回归系数 \(\beta = (\beta_1, ..., \beta_p)^T\) 是对自变量的斜率。
因为线性模型的假设,所以在应用的时候需要进行模型诊断,才能决定适用性。模型诊断需要注意的地方包括:
- 标准化残差图
- 异常点
- 自相关性
- 多重共现性
7.2 线性模型预测房屋价格
ch6_house.csv 数据集记录了某地区 21613 座房屋的 10 个变量信息,我们据此可以建立线性模型预测房屋价格。
house 数据集的 10 个变量的定义如下:
- price:房屋价格
- bedrooms:卧室数目
- bathrooms:卫生间数目
- sqft_living:住房面积(平方英尺)
- sqft_lot:房基地面积
- floors:楼层数目
- condition:房屋整体状况的好坏,取值 1 - 5
- grade:房屋等级,取值 1 - 13
- sqft_above:除地下室以外的住房面积
- yr_built:房屋建成年份(最早 1900,最晚 2015)
library(readr)
file = xfun::magic_path("ch6_house.csv")
house = read_csv(file)
house## # A tibble: 21,613 × 10
## price bedrooms bathr…¹ sqft_…² sqft_…³ floors condi…⁴ grade sqft_…⁵ yr_bu…⁶
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 221900 3 1 1180 5650 1 3 7 1180 1955
## 2 538000 3 2.25 2570 7242 2 3 7 2170 1951
## 3 180000 2 1 770 10000 1 3 6 770 1933
## 4 604000 4 3 1960 5000 1 5 7 1050 1965
## 5 510000 3 2 1680 8080 1 3 8 1680 1987
## 6 1230000 4 4.5 5420 101930 1 3 11 3890 2001
## 7 257500 3 2.25 1715 6819 2 3 7 1715 1995
## 8 291850 3 1.5 1060 9711 1 3 7 1060 1963
## 9 229500 3 1 1780 7470 1 3 7 1050 1960
## 10 323000 3 2.5 1890 6560 2 3 7 1890 2003
## # … with 21,603 more rows, and abbreviated variable names ¹bathrooms,
## # ²sqft_living, ³sqft_lot, ⁴condition, ⁵sqft_above, ⁶yr_built
## # ℹ Use `print(n = ...)` to see more rows房屋价格变量本身是不符合正态分布的,将其进行转换后符合正态分布。(为什么?)
par(mfrow = c(2,2))
hist(house$price)
qqnorm(house$price)
hist(log(house$price))
qqnorm(log(house$price))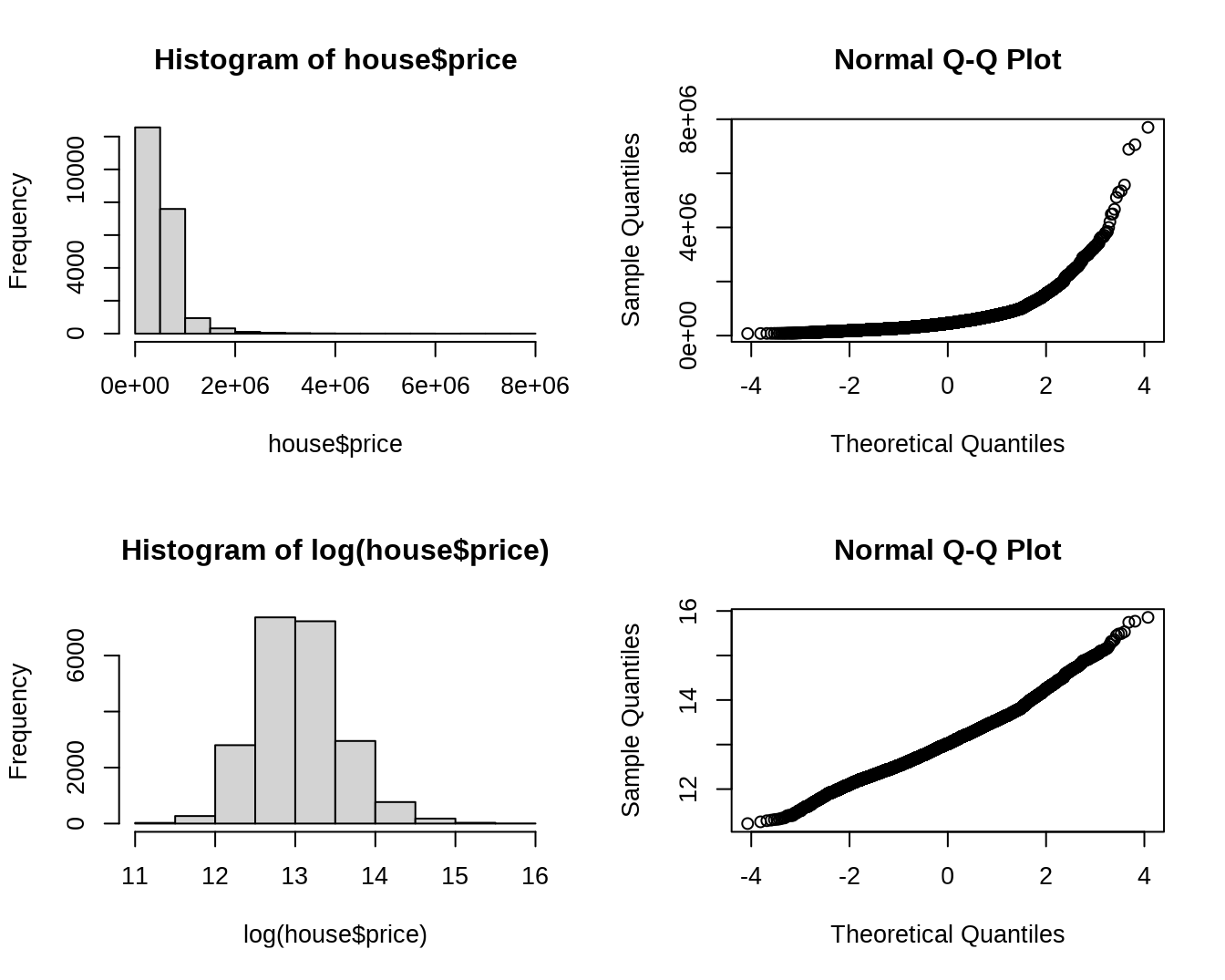
图 7.1: 转换前后房屋价格的直方图和 QQ 图
7.2.1 对房屋数据进行标准化
将 price、sqft_living 等变量均取对数。
同时,因为时间是无限增长的,在建模数据集中出现的时间不同于预测数据集中出现的时间,所以时间无法直接应用于建模。必须对时间变量进行转换。
library(dplyr)
varname = c("price", "sqft_living", "sqft_lot", "sqft_above")
house = house %>%
mutate(across(varname, log)) %>%
rename_with(~ paste0("log_",.x), .cols = varname) %>%
mutate(age = 2015 - yr_built) %>% # 对年份进行转换
select(-yr_built)将数据集随机划分为学习数据集和测试数据集。
7.2.2 拟合线性模型
对学习数据集建立线性模型。使用 summary() 查看模型系数的估计、残差的统计量、R 方等信息。从输出结果看,模型各自变量的贡献均比较显著,R 方值为 0.64。
##
## Call:
## lm(formula = log_price ~ ., data = house_learning)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.15983 -0.20963 0.01033 0.20339 1.65555
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 7.8340456 0.0732372 106.968 < 2e-16 ***
## bedrooms -0.0433545 0.0035877 -12.084 < 2e-16 ***
## bathrooms 0.0813344 0.0059163 13.748 < 2e-16 ***
## log_sqft_living 0.4887105 0.0160515 30.446 < 2e-16 ***
## log_sqft_lot -0.0332896 0.0034989 -9.514 < 2e-16 ***
## floors 0.0721198 0.0072678 9.923 < 2e-16 ***
## [ reached getOption("max.print") -- omitted 4 rows ]
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.3155 on 15119 degrees of freedom
## Multiple R-squared: 0.6406, Adjusted R-squared: 0.6404
## F-statistic: 2994 on 9 and 15119 DF, p-value: < 2.2e-16提取模型的系数估计值。
coefficients(fit.lm)## (Intercept) bedrooms bathrooms log_sqft_living log_sqft_lot
## 7.834045552 -0.043354513 0.081334366 0.488710493 -0.033289648
## floors condition grade log_sqft_above age
## 0.072119815 0.040946870 0.241517661 -0.076794423 0.006058074提取模型的系数置信区间,level = 0.95 表示提取 95% 置信区间。
confint(fit.lm, level = 0.95)## 2.5 % 97.5 %
## (Intercept) 7.690491718 7.977599387
## bedrooms -0.050386772 -0.036322253
## bathrooms 0.069737781 0.092930951
## log_sqft_living 0.457247630 0.520173356
## log_sqft_lot -0.040147996 -0.026431301
## floors 0.057873956 0.086365675
## condition 0.032523068 0.049370673
## grade 0.234395589 0.248639733
## log_sqft_above -0.106385018 -0.047203827
## age 0.005833631 0.006282517提取模型的因变量拟合值和残差。
7.2.3 线性模型的模型诊断
图 7.2 中:
左上是残差对拟合值的散点图。图中黑线表明,除了拟合值比较小的少部分数据点,残差的平均值接近于零,因而满足线性假设;对于不同的拟合值,残差围绕平均值变化的范围相当,因而满足同方差假设。
右上是标准化残差的正态 QQ 图。可以看出残差大致符合正态分布,但也有少数异常值偏离较大。
左下是标准化残差绝对值的平方根对拟合值的散点图,也可用于更方便的检查同方差假设是否成立。在本例中,大部分的数据点拟合值落在 [12, 15] 区间,在这一区间同方差假设是成立的(黑线水平,且黑线上下点的变化范围接近)。
右下是各观测的 Cook 距离图。从中可见,学习数据中的 5710 号观测点是异常点。
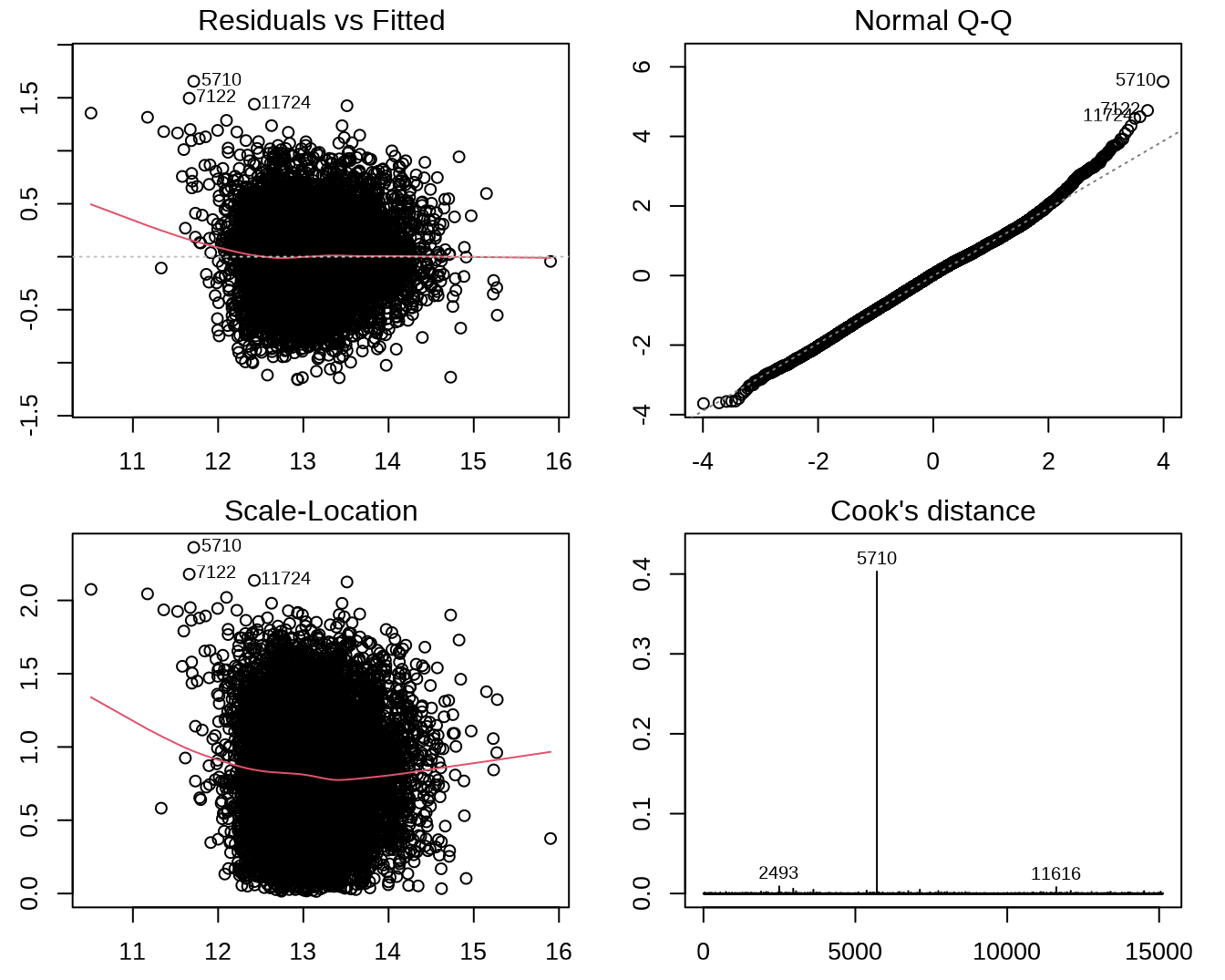
图 7.2: 对线性模型进行诊断。
7.2.4 优化线性模型
将异常点去掉,重新拟合线性模型。异常值就没有那么大了(图 7.3)。
fit2.lm = lm(log_price ~ ., data = house_learning[-5710,])
par(mfrow = c(2, 2),
mar = c(2.5, 2.5, 1.5, 1.5))
plot(fit2.lm, which = 1:4)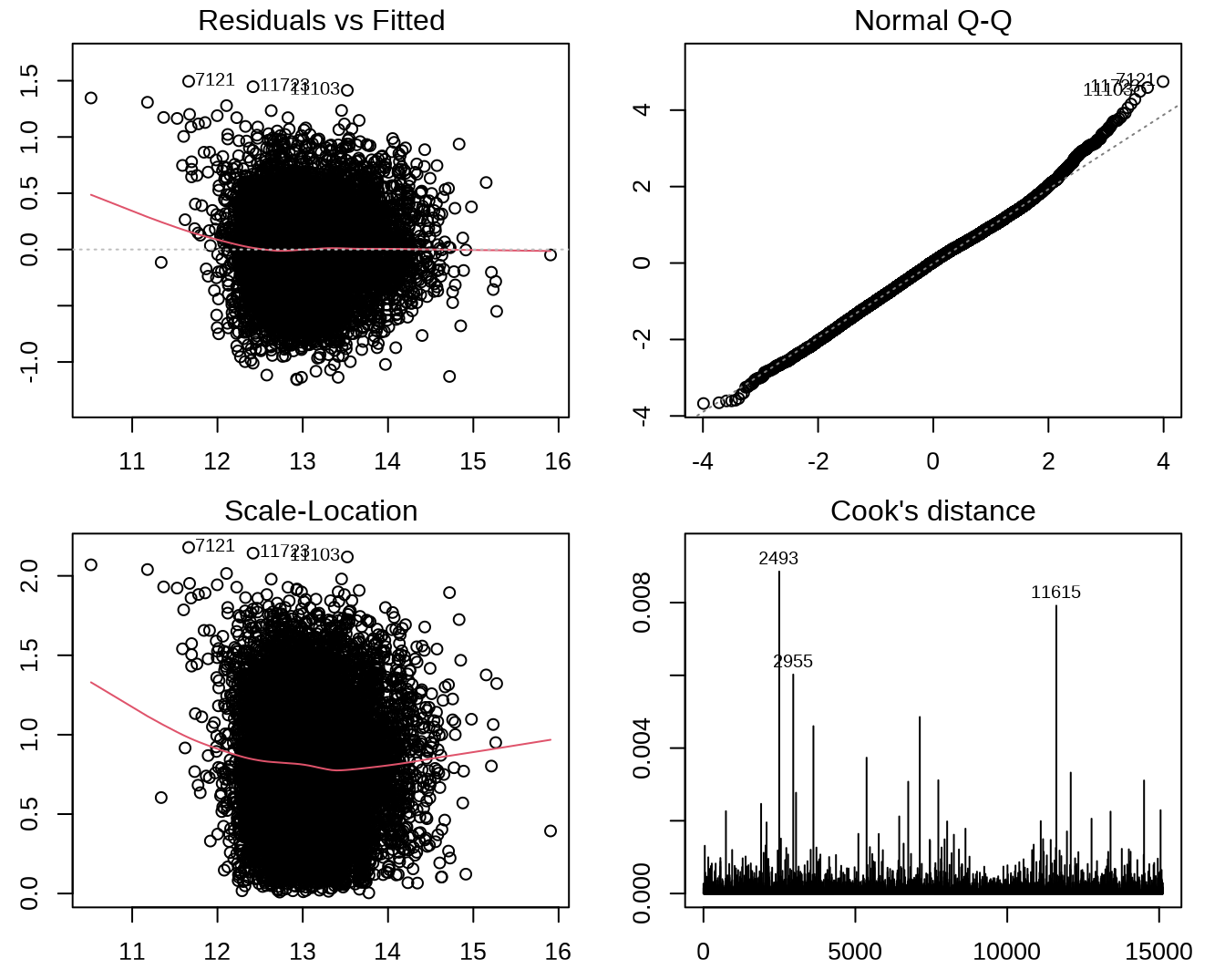
图 7.3: 对去除 1 个异常值后的新线性模型进行诊断。
使用所得的线性模型对测试数据集进行预测,计算均方根误差,查看预测价格与实际价格的偏差。
pred.lm = predict(fit2.lm, house_test)
# 均方根误差
rmse.lm = sqrt(mean((exp(pred.lm)-exp(house_test$log_price))^2))
# x 轴预测价格,y 轴实际价格
plot(exp(pred.lm), exp(house_test$log_price))
abline(a = 0, b = 1, col = "red")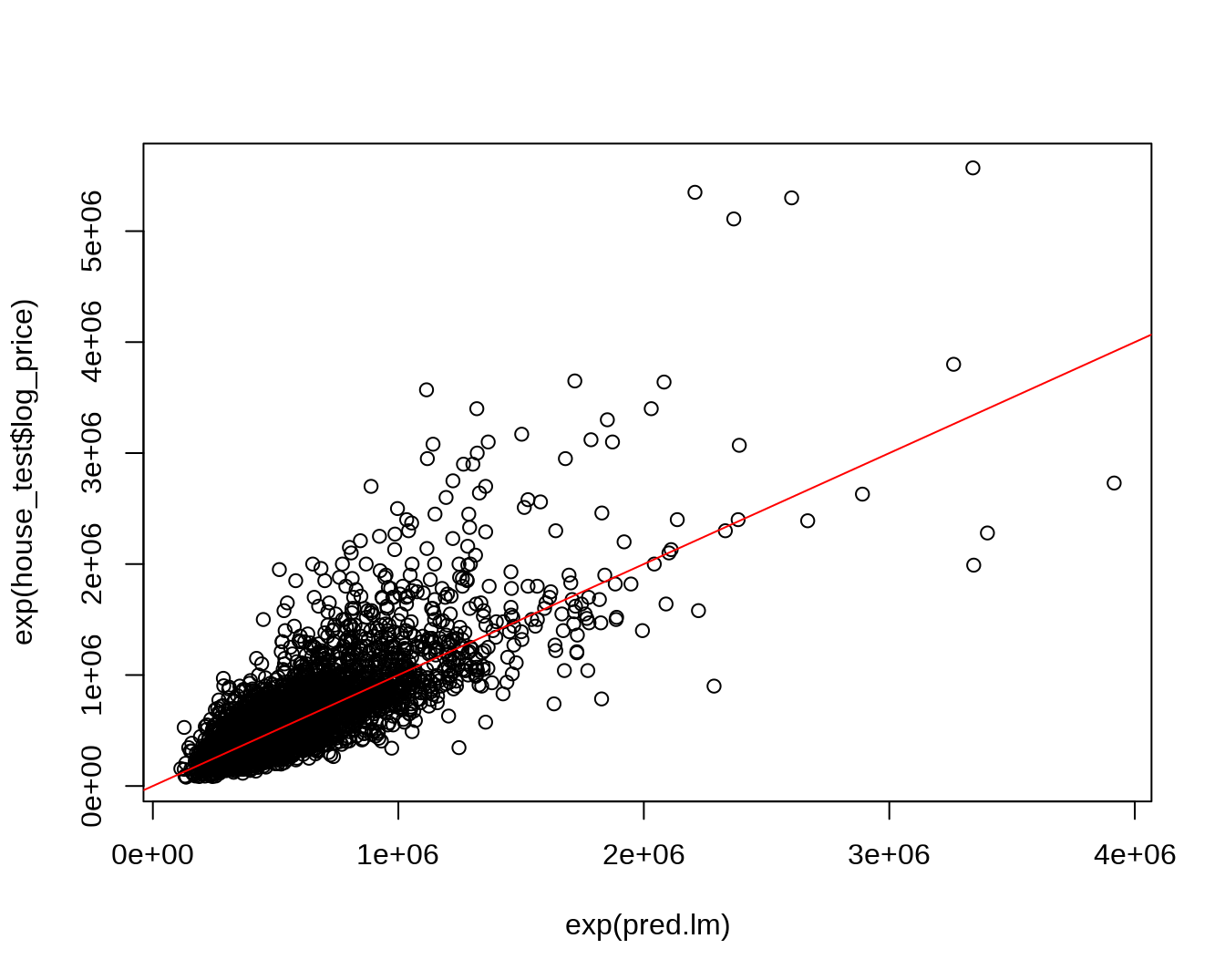
7.3 逻辑回归预测是否患糖尿病
ch6_diabetes.csv 数据集记录了 768 位印第安女性的糖尿病患病资料。
- Pregnacies:怀孕次数
- Glucose:餐后 2 h 血糖
- BloodPressure:舒张压(mmHg)
- SkinThickness:肱三头肌皮褶厚度(mm)
- Insulin:餐后 2 h 的胰岛素水平
- BMI:体重指数
- DiabetesPredigreeFunction:糖尿病谱系功能
- Age:年龄
- Outcome:因变量,1 表示有糖尿病,0 表示不患病。
file = xfun::magic_path("ch6_diabetes.csv")
diabetes = read_csv(file)
diabetes## # A tibble: 768 × 9
## Pregnancies Glucose BloodPressure SkinT…¹ Insulin BMI Diabe…² Age Outcome
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 6 148 72 35 0 33.6 0.627 50 1
## 2 1 85 66 29 0 26.6 0.351 31 0
## 3 8 183 64 0 0 23.3 0.672 32 1
## 4 1 89 66 23 94 28.1 0.167 21 0
## 5 0 137 40 35 168 43.1 2.29 33 1
## 6 5 116 74 0 0 25.6 0.201 30 0
## 7 3 78 50 32 88 31 0.248 26 1
## 8 10 115 0 0 0 35.3 0.134 29 0
## 9 2 197 70 45 543 30.5 0.158 53 1
## 10 8 125 96 0 0 0 0.232 54 1
## # … with 758 more rows, and abbreviated variable names ¹SkinThickness,
## # ²DiabetesPedigreeFunction
## # ℹ Use `print(n = ...)` to see more rows7.3.1 分层拆分糖尿病患病数据集
sampling(Tillé and Matei 2021) 包有各种抽样函数,可用于分层抽样将数据集分为学习数据集和测试数据集。这里使用 strata() 函数分层取 70% 的数据作为学习数据集。参数 stratanames 指定了分层变量的名字;参数 size 给出每层随机抽取的观测数;参数 method = "srswor" 说明在每层中使用无放回的简单随机抽样。
learning_sample$ID_unit 给出了抽样得到的结果,可用于获取拆分后的数据集。
set.seed(12345)
library(sampling)
diabetes = diabetes %>% # 分层抽样需要将分层变量排序后才能进行
arrange(Outcome)
learning_sample = strata(diabetes, stratanames = ("Outcome"),
size = round(0.7 * table(diabetes$Outcome)),
method = "srswor")
# 学习数据集
diabetes_learning = diabetes[learning_sample$ID_unit,]
# 测试数据集
diabetes_test = diabetes[-learning_sample$ID_unit,]7.3.2 模型拟合和验证
使用 glm() 拟合广义线性模型。family = "binomial" 指定了连接函数的类型(因变量分布为二项分布),从而得到一个 Logit 模型。
##
## Call:
## glm(formula = Outcome ~ ., family = "binomial", data = diabetes_learning)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.3442 -0.7207 -0.4096 0.7434 2.2946
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -8.289674 0.848811 -9.766 < 2e-16 ***
## Pregnancies 0.124052 0.038682 3.207 0.00134 **
## Glucose 0.037027 0.004547 8.144 3.83e-16 ***
## BloodPressure -0.017535 0.006206 -2.825 0.00472 **
## SkinThickness 0.005478 0.008023 0.683 0.49476
## Insulin -0.001491 0.001046 -1.426 0.15389
## [ reached getOption("max.print") -- omitted 3 rows ]
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 696.28 on 537 degrees of freedom
## Residual deviance: 505.64 on 529 degrees of freedom
## AIC: 523.64
##
## Number of Fisher Scoring iterations: 5将 Logit 模型应用于测试数据集对因变量进行预测。type = "response" 指定预测值为因变量取 1 的概率,并使用概率是否大于 0.5 为分界线,预测因变量类别为 1 或 0。
test.pred.logit = 1 * (predict(fit.logit, diabetes_test, type = "response") > 0.5)查看因变量真实值域预测值的列联表。真实值为 0(未患病)的有 134 例被预测为 0,16 例被预测为 1;真实值为 1(患病)的有 36 例被预测为 0,44 例被预测为 1。整个模型的预测准确性堪忧。
table(diabetes_test$Outcome, test.pred.logit)## test.pred.logit
## 0 1
## 0 134 16
## 1 36 44使用 LASSO 算法3 进行变量选择可以得到最佳模型。因为最佳模型与原模型的效果差别不大,所以不再赘述。
7.4 逻辑回归分析预测手机用户流失
本部分使用的移动运营商数据有多个数据集构成,分别记录了某移动运营商流失客户的信息和使用行为,以及未流失客户的信息和使用行为。
7.4.1 读取预处理好的数据集
在进行广义线性模型回归分析前,已经对数据进行了分层抽样,并将建模数据集分为学习数据集和测试数据集,并在学习数据集中通过欠抽样抽取了 10 个样本数据集 4。
# 读取 10 个学习数据集
learn = vector(mode = "list", 10)
for (k in 1:10){
file = xfun::magic_path(paste0("ch3_mobile_learning_sample", k, "_imputed.csv"))
learn[[k]] = read_csv(file, locale = locale(encoding = "GB2312")) %>%
arrange(`设备编码`)
}
# 读取 10 个测试数据集
test = lapply(1:10, function(k){
paste0("ch3_mobile_test_sample", k, "_imputed.csv") %>%
xfun::magic_path() %>%
read_csv(locale = locale(encoding = "GB2312")) %>%
arrange(`设备编码`)
})7.4.2 建立(均值)逻辑回归模型
根据学习数据集的每个插补后样本数据集建立逻辑模型。使用去掉 设备编码 后的数据集为输入,以 是否流失 为因变量,其它变量为自变量,family = "binomial" 指定因变量分布为二项分布。
library(glmnet)
fit.logit = lapply(1:10, function(k){
# 逻辑回归模型
glm( `是否流失` ~ .,
data = learn[[k]] %>% select(-`设备编码`),
family = "binomial")
})将根据学习数据集的 10 个插补后数据集分别建立模型所得的 10 组预测流失概率进行平均,得到测试数据集的预测流失概率。
7.4.3 计算逻辑回归模型预测的准确率
生成列联表后,分别计算模型预测的准确率。
class.logit = 1 * (prob.logit > 0.5)
conmat.logit = table(test[[1]][["是否流失"]], class.logit)
conmat.logit## class.logit
## 0 1
## 0 4921 930
## 1 20 1367.5 LASSO 分析预测手机用户流失
接下来使用 LASSO 分析进行手机用户流失预测,并比较 LASSO 分析得出的模型与逻辑回归模型的准确性。
注意:LASSO 本身并不等价于线性模型,而是在针对多个变量建模时,为了简化线性模型,用来帮助选择线性模型变量的方法。
7.5.1 使用学习数据集建立 LASSO 回归模型
使用 10 个运营商数据插补生成的学习数据集进行建模。cv.glmnet() 对 glmnet 模型进行多重交叉验证,然后返回一个 cv.glmnet 类。该类不仅包括预测模型,还包括交叉验证中计算得到的多个成分。
cvfit.lasso = lapply(1:10, function(k){
# 只使用学习数据集中的自变量矩阵
x_learn = as.matrix(learn[[k]][, 2:58])
# 使用交叉验证选出调节参数 lambda 的最佳值
cv.glmnet(x_learn, learn[[k]][['是否流失']],
family = "binomial",
type.measure = "class")
})将模型应用于相应的插补后测试数据集进行预测,并计算 LASSO 模型的回归系数。
7.5.2 计算 LASSO 模型的预测准确率
计算 10 个 LASSO 模型平均的预测流失概率,并以概率 0.5 为阈值计算模型的预测准确率。
prob.lasso.mean = do.call("cbind", prob.lasso) %>%
rowMeans()
class.lasso = 1 * (prob.lasso.mean > 0.5)
conmat.lasso = table(test[[1]][["是否流失"]], class.lasso)
conmat.lasso## class.lasso
## 0 1
## 0 4919 932
## 1 18 138分别计算不同类型的预测准确度。
7.6 比较逻辑回归模型和 LASSO 模型
上面针对同样的运营商数据,分别建立了逻辑回归模型和 LASSO 模型,这两种模型得到的结果会有什么不同呢?接下来将回答这个问题。
7.6.1 模型预测准确率的差异
两种预测模型的准确率差异并不大。
accu = tibble(
type = c("未流失用户准确预测比例", "流失用户准确预测比例", "所有用户准确预测比例"),
logit = c(accu.y0.logit, accu.y1.logit, accu.logit),
lasso = c(accu.y0.lasso, accu.y1.lasso, accu.lasso)
)
accu## # A tibble: 3 × 3
## type logit lasso
## <chr> <dbl> <dbl>
## 1 未流失用户准确预测比例 0.841 0.841
## 2 流失用户准确预测比例 0.872 0.885
## 3 所有用户准确预测比例 0.842 0.8427.6.2 模型使用的自变量
根据方法的原理,可以得出 LASSO 模型使用的自变量可能会比逻辑模型要少一些。因此,下面分别分析每个 LASSO 模型纳入的自变量。
因为运营商数据包含的数据维度多达 57 个,所以在这些模型中实际上纳入的自变量可能是不同的,并且即便是两个模型纳入了同一个自变量,其在模型中的作用也可能是不同的。为了展示这种现象,这里将自变量系数区分为 3 类,大于 0,小于 0 和等于 0。
coef.indic.lasso = lapply(1:10, function(k){
coef.lasso[[k]][-1] %>% # 去掉截距项
t() %>%
as_tibble()
}) %>%
bind_rows() %>%
mutate_all( .funs = function(x) ifelse(x == 0, 0, ifelse(x > 0, 1, -1)))可以发现:在 10 个模型中,均为使用的变量就有 8 个,另外有其它变量被模型使用的次数在 1 - 9 之间,而被 10 个模型均纳入的变量只有 6 个。
超过 5 个模型选用的自变量有约 17 个,它们被不同模型使用的情况如下所示。
library(pheatmap)
library(RColorBrewer)
idx = which(colSums(abs(coef.indic.lasso)) > 5)
pheatmap(t(coef.indic.lasso[, idx]),
show_rownames = TRUE,
show_colnames = FALSE,
color = colorRampPalette(rev(brewer.pal(n = 7, name = "RdBu")))(100),
breaks = seq(-1, 1, length.out = 100))
实际上,即便不使用 LASSO 分析,在广义线性模型中也会报告有哪些自变量在模型中占有更高的权重。summary() 输出结果中的最后一列(Pr(>|z|)中,凡是小于 0.05 的都被特别标注了出来,这些便是模型中的主要参量。
summary(fit.logit[[1]])##
## Call:
## glm(formula = 是否流失 ~ ., family = "binomial", data = learn[[k]] %>%
## select(-设备编码))
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -3.15546 -0.38758 -0.00667 0.39992 2.87340
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 15.57839 12.23879 1.273 0.20306
## 彩铃费 1.19525 3.18991 0.375 0.70789
## 短信费 -0.40472 0.71838 -0.563 0.57318
## 本地语音通话费 -0.05480 0.31305 -0.175 0.86105
## 长途语音通话费 0.15550 0.40991 0.379 0.70442
## 省内语音漫游费 0.77114 0.38576 1.999 0.04561 *
## [ reached getOption("max.print") -- omitted 52 rows ]
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 1009.22 on 727 degrees of freedom
## Residual deviance: 434.86 on 670 degrees of freedom
## AIC: 550.86
##
## Number of Fisher Scoring iterations: 8